OEIS A181815

A 2010 sequence by Matt Vandermast.
Written by Michael Thomas De Vlieger, St. Louis, Missouri, 2021 0115.

Abstract.

We examine the reason behind the appearance of the plot of OEIS A181815, that is, as a “curtain of fractal spray” noted by Antti Karttunen 28 December 2019.

Introduction.

Let primorial P(n) = A2110(n) = the product of the smallest n prime numbers, thus, P(4) = p₁ × p₂ × p₃ × p₄ = 2 × 3 × 5 × 7 = 210. The sequence begins:

1, 2, 6, 30, 210, 2310, 30030, 510510, 9699690, ...

We recognize the standard form of prime decomposition (D):

n = p₁^e1 × p₂^e2 × … × p_w^ew
(integers) such that primes p₁ < p₂ < … < p_w.

Here, w = ω(n) = A1221(n), the number of distinct primes p | n.

Define a “prime signature” M(n) as the multiset of multiplicities e seen in D(n), usually sorted greatest to least. Hence, for the number n = 504 = 2³ × 3² × 7¹ = p₁³ × p₂² × p₄¹ (in the form where the subscript i represents π(p) = A720(p), the index of prime p), M(504) = {3, 2, 1}. We may note zeros in M(n) so as to preserve the index i of each prime, evoked according to the position in the list, hence we may list according to row n of A067255, hence, A067255(504) = {3, 2, 0, 1}. We can add any number of zeros to the list as regards prime signature, since zeros in the list represent the empty product, thus we do not list zeros in a prime signature. We note that the prime signature is tantamount to an ordered list of multiplicities of the diverse primes p | n, hence M(n) is a multiset, since we may have more than one listed multiplicity. For instance, M(10) = {1, 1}, a recipe we first encounter for n = 6; this recipe is often referred to as the squarefree semiprimes A6881, which begins, {6, 10, 14, 15, 21, 22, 26, 33, 34, 38, …}. We go on to say that M(p) = {1} and M(P(n)) presents a list of any number of 1s.

Consider s(n) = A025487(n), the sequence that lists products of primorials. As a consequence of this definition, we have numbers m that are products that are products of the smallest w = ω(s(n)) primes p_i^e where multiplicity e > 0. We note that M(504) = {3, 2, 1} might be interpreted such that we ascribe prime power p_i^ei to the multiplicity e_i found at position i, hence read the number as p₁³ × p₂² × p₃¹ = 2³ × 3² × 5¹ = 360. We sort the multiplicities greatest to least to obtain the smallest possible m with this prime signature. Hence, n = 2025788 = 2² × 17¹ × 31³, which shares the same prime signature, would similarly boil down to 360 given the aforementioned interpretation. Therefore, the number m = 360 appears in s and is emblematic of all numbers with M(n) = {3, 2, 1}, that is, the product of a cube of a prime, a square of a different prime, and a third prime. Therefore we may also regard s(n) as a list of m that are the least numbers of a given prime signature.

Note that m in s(n) has two principal parameters, w = ω(m), the number of distinct prime divisors p_i | n for 1 ≤ i ≤ w, and ℓ = A7814(m) = 2-adic valuation of m since all the prime power multiplicities e are nonincreasing as i increases.

The sequence s begins:

1, 2, 4, 6, 8, 12, 16, 24, 30, 32, 36, 48, 60, 64, 72, 96, 120, 128, 144, 180, 192, 210, ...

We note that all least terms of prime signatures, m ≤ P(k) occur in s, hence we may generate s in an algorithmic way delimited by P(k). Thus it is natural to delimit the sequence s by primorials P(k) and thus derive datasets of lengths in A098719. This sequence begins:

1, 2, 4, 9, 22, 54, 114, 246, 488, 948, 1809, 3327, 6020, 10624, 18246, 30726, 51148, 84074, 135598, 216398, 340886, 529051, 814237, 1240172, 1874464, 2817289, 4195918, 6186286, 9049492, 13121704, 18895821, 27199504, 38892092, 55318849, 78130780, 110028527, ...

We define a “multiplicity diagram” as a sort of histogram that portrays the multiplicities listed in row n of A067255 in column i for the prime power factor p_i^ei. When gcd(p_i , n) = 1, we leave the column i blank.

Figure 1 is a set of labeled multiplicity diagrams that pertain to the smallest terms of s = A025487:

We note that the conjugate of M(n) or M(n)* is a list of indices of primorials that produce n. Hence, for n = 60 = 2² × 3¹ × 5¹, with M(60) = {2, 1, 1}, the conjugate {3, 1} (for 3 primes with e ≥ 1, and 1 prime with e ≥ 2) signifies that 60 = P(3) × P(1) = 30 × 2. We may state all m in s(n) either as the product of all prime powers p_i^e for 1 ≤ i ≤ ω(m) and e > 0, or rather, the product of primorials of a multiset of indices. The sequence A181822 transforms A025487(n) into the number m produced by interpreting M(m)* as if it were M(m). For instance, the number m = 24 = 2³ × 3¹ ⇒ 2² × 3¹ × 5¹ = 60, and conversely, 60 ⇒ 24.

It is clear that there exist some m such that M(m) is self-conjugate, meaning that M(m) = S = M(m)*. An example is m = 360 = 8 × 9 × 5 = 2³ × 3² × 5¹ = P(3) × P(2) × P(1) = 30 × 6 × 2.

Now we regard M(m)* = {k₁, k₂, …, k_ℓ} for 1 ≤ j ≤ ℓ and suppose we interpret each k instead as p_k and take the product. Since the exponents e_i of primes p_i^ei | m are nonincreasing as i increases, we know that ℓ = A7814(m) = 2-adic valuation of m. Hence, M(24)* = {2, 1 ,1} ⇒ p₂ × p₁ × p₁ = 3 × 2 × 2 = 12. The greatest prime factor A6530(m) = gpf(m) is the function that converts the factors P(k) | m → p_k | m'. We thus define the sequence described immediately below.

Primorial decomposition of A025487(n) remapped to primes.

Let a(n) = A181815(n) = largest integer m such that for all d | m, A025487(n)/d = q ∈ A025487.

The sequence begins:

1, 2, 4, 3, 8, 6, 16, 12, 5, 32, 9, 24, 10, 64, 18, 48, 20, 128, 36, 15, 96, 7, 27, 40, 256, 72, 30, 192, 14, 54, 80, 512, 144, 60, 384, 28, 108, 25, 160, 1024, 45, 288, 21, 81, 120, 768, 56, 216, 50, 320, 2048, 90, 576, 11, 42, 162, 240, 1536, 112, 432, 100, 640, 4096, 180, 1152, 22, 84, 324, 75, 480, 3072, 35, 135, 224, 864, 200, 63, 1280, 243, 8192, 360, 2304, 44, 168, 648, 150, 960, 6144, 70, 270, 448, 1728, 33, 400, 126, 2560, 486, 16384, 720, 4608, 88, 336, 1296, 300, 1920, 12288, 140, 540, 896, 125, 3456, 66, 800, 13, ...

As shown in the OEIS entry, the sequence is a permutation of the natural numbers with a delightful serpent-scale-like logarithmic plot. τ(a(n)) = number of ordered factorizations of s(n) as s( j) × s(k), Cf. A182762. The sequence rearranges terms of A108951 into ascending order, as A108951(a(n)) = s(n).

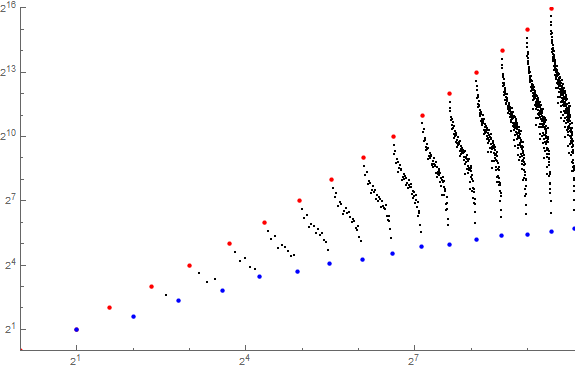
Figure 2 is a log plot of a(n) for 1 ≤ n ≤ A098719(10) = 1805, highlighting records in red, and local minima in blue. Many of the records are labeled log₂ a(n), while many of the local minima are labeled π(a(n)).

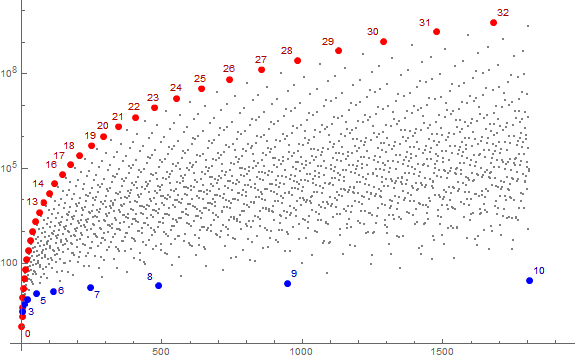
We note that m = 2ⁿ for n ≥ 0 in a(n) sets records at indices r(n+1) = A025488(n+1).

The sequence r(n) begins:

1, 2, 3, 5, 7, 10, 14, 18, 25, 32, 40, 51, 63, 80, 98, 119, 145, 173, 207, 248, 292, 346, 404, 473, 552, 639, 742, 855, 984, 1129, 1289, 1477, 1681, 1912, 2170, 2452, 2771, 3121, 3514, 3951, 4426, 4955, 5536, 6182, 6898, 7674, 8535, 9470, 10500, ...

Relating a(n) to integer partitions interpreted as prime signatures.

Observe that for s(n) = 2^N, a(n) = 2^N, since, though M(2^N) = {N}, M(2^N)* is a list of N 1s, thus, again 2^N under the transformation rules for a(n). Suppose we maintained the total number N of primes p in family F, but, recognizing we might only shift multiplicity to the next largest primes, we find that the shape M(2^N) is the least, thus first-occurring in s among the family F of shapes that have N primes, i.e., F(N). Hence we know that those F(N) primes appear first for 2^N and last for P(N), and thus numbers in F with N primes makes an appearance in s ahead of numbers in F with (N + 1) primes, the first of which occurs for 2^{(N + 1)} > 2^N. Furthermore, though other numbers in F with N primes proves to exceed M(2^N), in a(n), we transform some of the factors 2 that result from M(2^N)* into larger factors, moving to 3, then to 5, etc. We find that none of the products we can furnish via f(M*) for numbers in F(N) is nearly as large as the product m = f(M(2^N)*). Hence, the records of a(n) are 2^N at indices in A025488(N+1).

Figure 3 shows all prime shapes M with N = 5 primes p, distributed such that they occur in s. The multiplicity notations M in {{5}, {4, 1}, {3, 2}, {3, 1, 1}, {2, 2, 1}, {2, 1, 1, 1}, {1, 1, 1, 1, 1}} are indeed the integer partitions of 5. These, interpreted as M equate to 32, 48, 72, 120, 180, 420, and 2310, respectively.

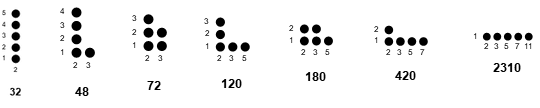
Family F(N) is row N in A036035.

Let’s explore the transformation of these m such that M(m) derive from the integer partitions λ of N = 5 (the 1 ≤ k ≤ 7 partitions λ in row 5 of A080577). We obtain λ as a list of addends (e₁, e₂, …, e_i, …, e_w), but instead interpret the parts e as the exponents of the i-th prime to obtain the product Π_{i=1..w} p_i^ei. This defines m = A025487(c).

These numbers m are transformed as follows in Table 1:

k      m   M(m)        M(m)*   a(c)              c
--------------------------------------------------
1     32   5  ->   1.1.1.1.1 ->  2×2×2×2×2 = 32   10
2     48   4.1  ->   2.1.1.1 ->  3×2×2×2   = 24   12
3     72   3.2   ->    2.2.1 ->  3×3×2     = 18   15
4    120   3.1.1  ->   3.1.1 ->  5×2×2     = 20   17
5    180   2.2.1   ->    3.2 ->  5×3       = 15   20
6    420   2.1.1.1  ->   4.1 ->  7×2       = 14   29
7   2310   1.1.1.1.1  ->   5 ->  11        = 11   54

We obtain the 7 partitions of 5. Starting with the first:

1. (5) is read instead as 2⁵ = 32, which appears in A025487 at c = 10. Taking the conjugate M(32)* gives us 1.1.1.1.1, and interpreting each part j instead as the j-th prime, we have 2 × 2 × 2 × 2 × 2 = 2⁵ = 32. Thus, a(10) = 32.

2. (4+1) is read instead as 2⁴ × 3¹ = 48, which appears in A025487 at c = 12. Taking the conjugate M(48)* gives us 2.1.1.1, and interpreting each part j instead as the j-th prime, we have 3 × 2 × 2 × 2 = 24.

3. (3+2) is read instead as 2³ × 3² = 72, which appears in A025487 at c = 15. Taking the conjugate M(72)* gives us 2.2.1, and interpreting each part j instead as the j-th prime, we have 3 × 3 × 2 = 18.

4. (3+1+1) is read instead as 2³ × 3¹ × 5¹ = 120, which appears in A025487 at c = 17. Taking the conjugate M(120)* gives us 3.1.1, and interpreting each part j instead as the j-th prime, we have 5 × 2 × 2 = 20.

5. (2+2+1) is read instead as 2² × 3² × 5¹ = 180, which appears in A025487 at c = 20. Taking the conjugate M(180)* gives us 3.2, and interpreting each part j instead as the j-th prime, we have 5 × 3 = 15.

6. (2+1+1+1) is read instead as 2² × 3¹ × 5¹ × 7¹ = 420, which appears in A025487 at c = 29. Taking the conjugate M(420)* gives us 4.1, and interpreting each part j instead as the j-th prime, we have 7 × 2 = 14.

6. (1+1+1+1+1) is read instead as 2¹ × 3¹ × 5¹ × 7¹ × 11¹ = 2310, which appears in A025487 at c = 54. Taking the conjugate M(2310)* gives us 5, and interpreting each part j instead as the j-th prime, we have 11.

As a rule, regarding N, the partitition λ = (N) transforms to 2^N, while the partition of ones transforms to p_N. Take A080577 as an irregular tetrahedron T(n,k) where λ_n,k is the k-th partition of n and the length of row n = p(n) = A41(n). T(n,k) lists the partitions of n in reverse lexical order, thus (n) appears at k = 1, while (1+…+1) appears at k = p(n). If we interpret each part i in λ_n,k instead as the exponent of the i-th prime, hence p_i^ei, we find that row n includes a range of products 2ⁿ through P(n) that generally increase. Under the transformation in sequence a, we instead have row n include a range of products 2ⁿ through p_n that generally decrease. The primorial P(n) transforms into the prime p_n while 2ⁿ is idempotent. Hence the greatest term produced by reading λ as a prime signature becomes the least term in the transformation to sequence a.

Furthermore, the effect of the transformation in sequence a is to arrange the products m' in ranks based on gpf(m') within the family F. We see that gpf(m') = p_ω(m).

Now we see that the conjugate M(m)* might have instead derived not from m (which is the product of the parts e_i of λ_n,k read instead as exponents of p_i^ei), but of the conjugate partition λ_{n, (p(n)−k)}. Since the transformation of sequence a is taking the product of the parts j read instead as p_j, we see that we are taking the Heinz number of λ_{n, (p(n)−k)}.

Hence, in family F(N), we have converted the terms of row N in A036035 to the corresponding term in row N of A333485.

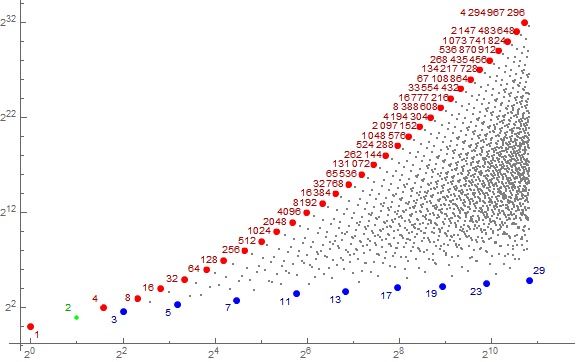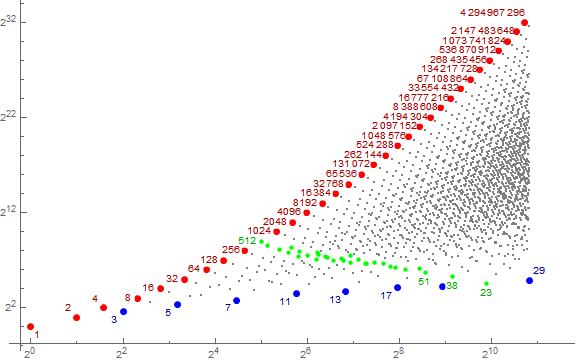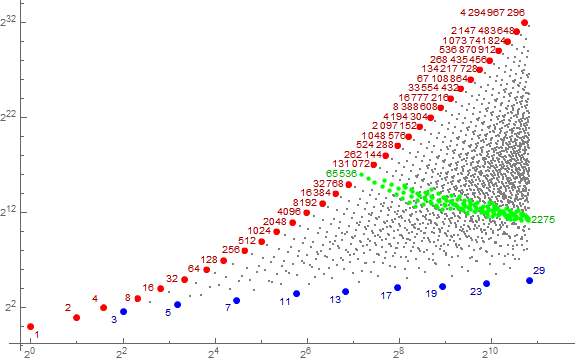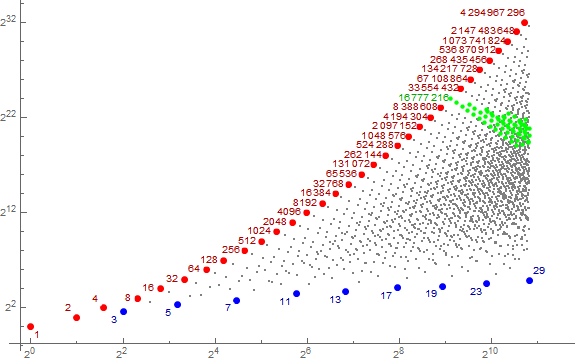
Figure 4 is a log plot of a(n) for 1 ≤ n ≤ A098719(5) = 54 as in Figure 2, but here showing the family F(5) in green.

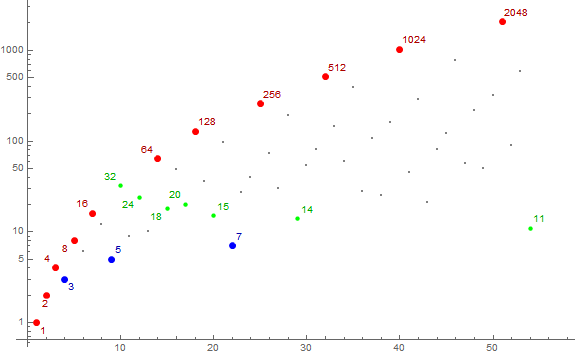
Figure 4 illustrates the bijection between 2^N and p_N, where all the terms m with Ω(m) = N array in a ranked path between them. For small N, the paths appear more or less linear and do not interfere with one another. However, as N increases the m in the family appear among terms of other families.

We can thus determine some “lengthwise” patterns or trajectories of certain primeshapes in sequence a. Obvious trajectories pertain to 2^N and p_N, where the former appear as maxima and the latter local minima. We can also find 3 × 2^(N−1) running just below 2^N. With diligence, we can trace sundry trajectories and explain the plot of A181815 this way.

Therefore, for family F(N), we convert t_n,k of A036035 to u_n,k in A333485.

Figure 5 is a log-log plot of rows 1 ≤ N ≤ 16 of A036035, highlighting primorials P(N) in blue and 2^N in red.

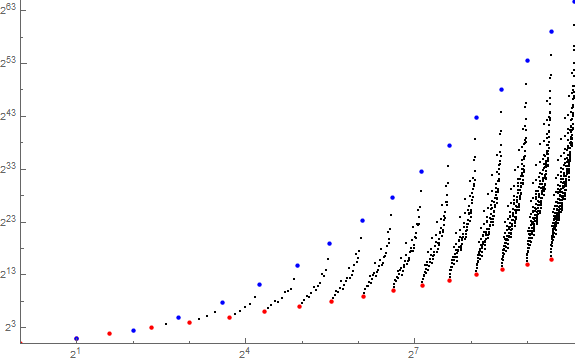
Figure 6 is a log-log plot of rows 1 ≤ N ≤ 16 of A333485, highlighting primorials p_N in blue and 2^N in red.

The difference between A333485 and a(n) is that the latter places m according to the index c in A025487 where m → π(p_e) sorted greatest to least, interpreted as Π_{i=1.. Ω(m)} p_i^ei. Therefore we have an intercalated arrangement of the families F(N) in a(n), whereas in A333485, the families F(N) are set into distinct rows N.

Figure 7 is an animated log-log plot of a(n) for 1 ≤ n ≤ A098719(10) = 1809 cycling through the families F(N) for 1 ≤ N ≤ 24 in green.

The animated plot illustrates how the families F(k) sweep out the plot as k increases. The “texture” results from the product of the configuration of primes p seen in the integer partitions row k of A080577 read instead as if row k of A067255.

Hence, it appears that we have determined the reason for the texture exhibited by the plot of A181815.

Appendix:

Code Toolbox: Here are a few scripts that aid in generating or analyzing this sequence:

Multiplicity notation:

A067255[n_] := If[n == 1, {0},
  ReplacePart[Table[0, {PrimePi[f[[-1, 1]]]}], #] &@
    Map[PrimePi@ First@ # -> Last@ # &, #]] &@ FactorInteger@ n]

(Simple) conjugate*:

conj[w_] := Table[LengthWhile[#1, # >= j &], {j, #2}] & @@ {w, Max[w]}

* This conjugate program works only in cases given nonincreasing input.

Fast generation of all terms of A025487 less than and including A2110(n)*:

A025487[n_] := {{1}}~Join~
  Block[{lim = Product[Prime@ i, {i, n}],
   ww = NestList[Append[#, 1] &, {1}, n - 1], dec},
   dec[x_] := Apply[Times, MapIndexed[Prime[First@ #2]^#1 &, x]];
   Map[Block[{w = #, k = 1},
      Sort@ Prepend[If[Length@ # == 0, #, #[[1]]],
        Product[Prime@ i, {i, Length@ w}] ] &@ Reap[
         Do[
          If[# < lim,
             Sow[#]; k = 1,
             If[k >= Length@ w, Break[], k++]] &@ dec@ Set[w,
             If[k == 1,
               MapAt[# + 1 &, w, k],
               PadLeft[#, Length@ w, First@ #] &@
                 Drop[MapAt[# + Boole[i > 1] &, w, k], k - 1] ]],
           {i, Infinity}] ][[-1]] ] &, ww]]

* Requires flattening and taking union so as to appear as a list.

Code 1: Generate a(n):

a181815 = Map[Times @@ Prime@ conj@ A067255[#] &, Union@ Flatten@ A025487@ 12];

Code 2: Generate A333485(n):

{1}~Join~Flatten@ Array[Times @@ Prime@ conj@ # & /@ IntegerPartitions[#] &, 25]

Concerns OEIS sequences:

A000040: The primes p_n.
A000041: Number of partitions of n.
A000079: 2ⁿ.
A000244: 3ⁿ.
A002110: The primorials.
A003961: Completely multiplicative Π( p_i^ei ) → Π( p_(i+1)^ei).
A005408: The odd numbers 2ⁿ + 1.
A006530: Greatest prime divisor of n, gpf(n).
A025487: Numbers that are products of primorials, also, least m of a given prime signature.
A025488: Number of distinct prime signatures of the positive integers up to 2ⁿ.
A034386: Product of primes q ≤ n.
A036035: Least integer of each prime signature, in graded (reflected or not) colexicographic order of exponents.
A062755: Row n = prime signature of n noting only multiplicities, where prime p_k is maintained by placeholder zeros.
A080577: Row n = Integer partitions of n.
A098719: Index of the n-th primorial A2110(n) in A025487.
A108951: Primorial inflation of n: Fully multiplicative with a(p) = P(p) for prime p, where P(x) is the primorial A034386(x).
A181815: Numbers where all prime divisors are consecutive primes starting at 2.
A181822: Numbers that result from interpreting M(n)* as a prime composition.
A333485: Heinz numbers of all integer partitions sorted first by sum, then by decreasing length, and finally lexicographically.

Document Revision Record.

2021 0115 1700 Draft 1.
2021 0209 1645 Final.
2021 0210 1730 Add code.

Click here for the index to other work.