Consecutive numbers of certain omega-multiplicity species.

Michael Thomas De Vlieger, St. Louis, Missouri, 2022 1123.

Abstract.

Mathematicians have long considered certain curios regarding the spacing and adjacency of primes and their powers. We know that {2, 3} are the only adjacent primes. Catalan conjectured and Mihăilescu proved that {8, 9} are the only adjacent multus numbers (composite prime powers). This paper explores curios associated with the other omega-multiplicity [1] species.

Introduction.

Let us recall the five principal divisions of the natural numbers based on one or many distinct prime factors, and regarding multiplicity of such prime factors, all prime factors limited to multiplicity 1 or more than 1. We set aside {1} as the empty product.

Everyone is familiar with prime numbers (OEIS A40) as numbers that are divisible by themselves and 1, having precisely 2 divisors. Those numbers outside the empty product and the primes are called composite (A2808).

Numbers that have only 1 distinct prime factor are called prime powers (A961). Therefore, we may distinguish the primes from these to create a sequence A246547 = A961 \ A40 that we call “multus” [1].

Numbers that have at most 1 copy of any given distinct prime factor are called squarefree numbers (A5117). Again, we may strain out the primes and create a sequence of “varius” numbers A120944 = A5117 \ A40 [1].

The numbers that are neither squarefree nor prime power we call “tantus” numbers A126706.

Finally, we recognize numbers that are multiples of more than 1 multus number, called “plenus” numbers, A286708. Together, the empty product, multus, and plenus numbers comprise the powerful numbers A1694 = ∪({1}, A246547, A286708).

Consecutive prime numbers.

The primes 2 and 3 are the only adjacent numbers. 2 is the smallest prime, and 3 the second-smallest. Since every other number (the even numbers) are divisible by 2, larger primes must be odd and therefore have at least one composite number between them. When only 1 composite number separates primes, they are called twin primes. This has long been understood and we contribute nothing new to the understanding of the adjacency and spacing of primes.

Consecutive multus numbers.

In 1844, Eugène Catalan conjectured that {8, 9} are the only consecutive multus numbers, though of course he never used the term; instead these were called consecutive prime powers. If the latter phrase is used, then we should recognize that there are two such adjacent pairs: {2, 3} and {8, 9}, however the understanding goes beyond strict semantics. Preda Mihăilescu proved the conjecture in 2002. Given Mihăilescu’s theorem, nothing more seems to need to be added to what we know about the adjacency of multus numbers.

Let D_M = A053707(2..) be the sequence of first differences of A246847. This sequence begins as follows:

4, 1, 7, 9, 2, 5, 17, 15, 17, 40, 4, 3, 41, 74, 13, 33, 54, 18, 151, 17, 96, 104, 112, 120, 63, 307, 38, 312, 168, 199, 139, 10, 12, 192, 408, 316, 356, 240, 375, 393, 424, 128, 288, 912, 320, 298, 30, 1032, 271, 1217, 792, 408, 840, 432, 286, 602, 1872, 984, 504, 255, 423, 354, 1608, 552, ...

We find curious the occasion of many near-prime powers among arbitrary data near the end of a sequence of 83640 terms, such as 8386872 and 4194288. This remains to be investigated.

This sequence has an interesting scatterplot. Tony Noe remarks on its appearance in comments at OEIS: “In the graph of this sequence, the lowest curve corresponds to differences of squares of twin primes; the next-lowest curve is for squares of adjacent primes differing by 4, etc.”

Figure 1: scalar scatterplot of 83640 terms of A053707, manifesting the lines Noe described.

Consecutive varius numbers.

Since 2² | m for m mod 4 ≡ 0, runs of consecutive squarefree numbers are limited to 0 ≤ ℓ ≤ 3, with 3 common for small m. The smallest instances of ℓ are summarized in Table 1.

Table 1. First occurrences of runs of ℓ consecutive squarefree numbers.

ℓ   run with squarefree numbers bracketed.
----------------------------------
0   4(211)+(1..3) = 845, 846, 847.
1   4(6)+(1..3)   = 25, [26], 27.
2   4(2)+(1..3)   = 9, [10, 11].
3   4(0)+(1..3)   = [1, 2, 3].

Define C_S(n) = |m| ∈ {4n+1…4(n+1)−1} : m is squarefree ∧ n ≥ 0.

Generally this sequence begins as follows:

3, 3, 2, 3, 2, 3, 1, 3, 3, 3, 3, 2, 1, 2, 3, 2, 3, 3, 2, 3, 2, 3, 2, 3, 1, 3, 3, 3, 3, 2, 2, 1, 3, 2, 3, 3, 2, 2, 2, 3, 2, 3, 1, 2, 3, 3, 3, 2, 3, 2, 3, 2, 3, 3, 3, 3, 2, 3, 2, 3, 1, 2, 2, 3, 3, 2, 3, 2, 2, 2, 3, ...

We consider these runs without primes and the empty product. The same limitation according to mod 4 applies to the runs of consecutive various numbers:

ℓ   run with varius numbers bracketed.
----------------------------------
0   4(0)+(1..3)   = 1, 2, 3.
1   4(1)+(1..3)   = 4, 5, [6].
2   4(3)+(1..3)   = 13, [14, 15].
3   4(8)+(1..3)   = [33, 34, 35].

The smallest instance of ℓ = 3 is {33, 34, 35}.

Define C_V(n) = |m| ∈ {4n+1…4(n+1)−1} : m is varius ∧ n ≥ 0.

The sequence C_V begins as follows:

0, 1, 1, 2, 0, 2, 1, 1, 3, 2, 1, 1, 1, 1, 2, 1, 2, 2, 1, 2, 1, 3, 1, 3, 0, 1, 2, 2, 2, 2, 2, 0, 2, 2, 1, 3, 2, 0, 2, 2, 1, 2, 1, 1, 2, 2, 3, 1, 2, 0, 3, 2, 2, 3, 3, 2, 1, 2, 1, 2, 0, 2, 1, 3, 2, 1, 3, 0, 2, 1, 1, ...

Since we may have no squarefree numbers between numbers m mod 4 ≡ 0, or indeed, even consecutive multiples of 4 with no squarefree numbers between them, we may have a displacement between numbers in A5117 that exceeds 4.

Sequence A076259 contains first differences of A5117, while A020753 gives successive record gap lengths between squarefree numbers and A045882 is the first term of a run of at least n consecutive non-squarefree numbers. A045882 begins as follows:

4, 8, 48, 242, 844, 22020, 217070, 1092747, 8870024, 221167422, 221167422, 47255689915, 82462576220, 1043460553364, 79180770078548, 3215226335143218, 23742453640900972, 125781000834058568, ...

We can create an analog to each of these sequences regarding the varius numbers m ∈ A120944. We define D_V as the first differences of A120944, and find records and their indices in this sequence. We define the sequence L_V as an analogy to A045882 but pertaining instead to varius numbers. Table 2 summarizes findings given 9121429 terms of A120944, that is, all varius m ≤ 2²⁴:

 ℓ        k  A120944(k)+1
----------------------
 1        3         15
 2       17         56
 3        8         31
 4        1          7
 5       15         47
 6        4         16
 7       35         96
 8       56        147
 9    41331      81043
10    13842      27732
11   105888     204323
12   508340     960642

Hence the first terms of L_V begin as follows:

15, 56, 31, 7, 47, 16, 96, 147, 81043, 27732, 204323, 960642, ...

Conjecture: We note that this sequence is perhaps organized by small numbers in the first 4 terms, larger ones in the second four, much larger in the third quartet. So we surmise, given the relevance of 4 as garantor of a non-varius number, that the next quartet will require numbers much larger than those of the third quartet, as it is hard to come by too many consecutive zeros in C_V.

Consecutive tantus numbers.

Tantus m ∈ A126706 are of the form p²k with p prime and k not a power of p. Therefore, m occurs densely in the residues r mod Q = p²k where k ≤ Q/p² for p|Q, and Q = A2110( j)² (i.e., Q in A061742), only interrupted by perfect powers of p. Using this principle we can produce a sieve-like diagram showing tantus m as 1 else 0.

The run length of consecutive tantus numbers seems to be only bounded by prime gaps. Therefore we consider the sequence D_T = A358089 of first differences of tantus numbers m ∈ A126706. In this sequence we observe the smallest numbers that start a run of exactly ℓ consecutive numbers in A126706, and note these in sequence A356322. The first terms of this sequence are as follows:

12, 44, 98, 3174, 844, 22020, 217070, 1092747, 8870024, 262315467, 221167422, 47255689915, 82462576220, 1043460553364, 79180770078548, ...

(See [2] for more on A356322.)

Consecutive plenus numbers.

We may cleave the powerful numbers A1694, ignoring the empty product, into two camps, one derived from the other.

The first camp is that of multus numbers m ∈ A246547, the composite prime powers, and the second are products of more than 1 multus number, that is, the plenus numbers m ∈ A286708. Plenus numbers have multiplicity exceeding 1 for all distinct prime divisors, hence they are a special case of tantus number and also appear in A126706. As an aside, the most efficient method of generating multus or plenus numbers is by straining one or the other out of the sequence of powerful numbers A1694 = { a²b³ : a ≥ 1 ∧ b ≥ 1}.

Having covered the first camp (multus numbers), we now examine first differences of A286708, which we store in OEIS A358173. This sequence begins as follows:

36, 28, 8, 36, 52, 4, 16, 9, 63, 36, 68, 8, 32, 9, 43, 16, 76, 72, 27, 1, 108, 16, 64, 36, 68, 4, 28, 89, 36, 27, 4, 69, 71, 27, 29, 20, 72, 77, 47, 32, 128, ...

This sequence has an interesting scatterplot that we can explain.

Figure 2: Scatterplot of A358173, showing subset S in red and R in blue.

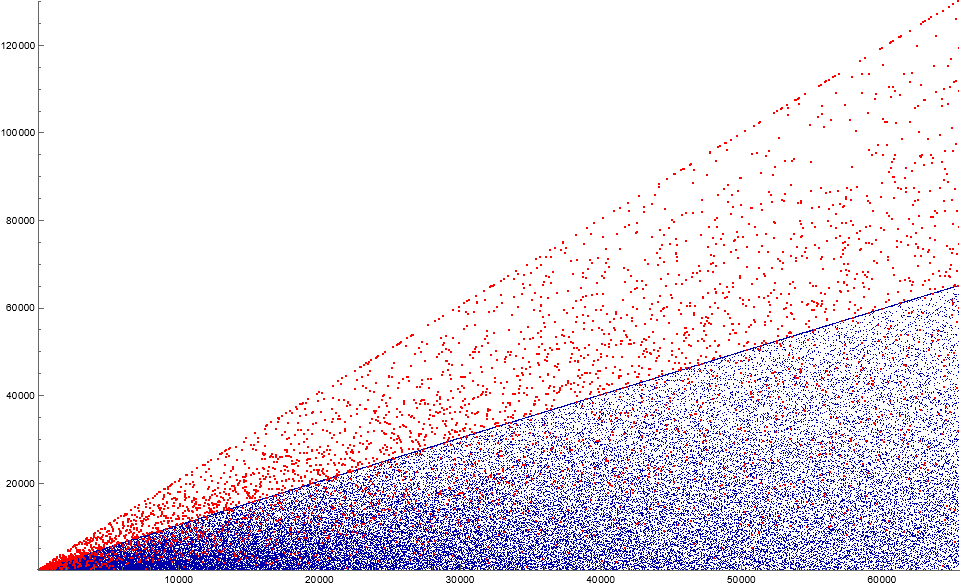
Consider the sequence of powerful numbers A1694 ⊃ A246547, the sequence of composite prime powers. Let s = A1694(k) such that ω(s) > 1 be followed by t = A1694(k+1) such that ω(t) = 1.

Since plenus A286708 = A1694 \ A246547, prime powers t are missing in A286708. We consider s = A286708( j) and note the following difference:

A286708( j+1) − A286708( j) > A1694(k+1) − A1694(k).

Therefore we see a subset S containing plenus numbers displaced with respect to the complementary subset R = A286708 \ S. some of this subset S (shown in red) exceeds the maxima of R (shown in blue) in the scatterplot of this sequence. The plot of the R resembles the scatterplot of A1694.

We turn to the first instance of m that begins a run of ℓ consecutive plenus numbers, having observed the first pair of consecutive plenus numbers are 675 = 3³ × 5² followed by 676 = 2² × 13². This sequence is A358174, which begins as follows:

675, 9800, 235224, 465124, 1825200, 11309768, 384199200, 592192224, 4931691075, 5425069447, 13051463048, 221322261600, 865363202000, 8192480787000, 11968683934831, 13325427460800, 15061377048200, 28821995554247, 48689748233307, 511643454094368, 1558709801289000, ...

Since plenus numbers are a form of tantus, sequence A358174 represents an intensification of axioms of A356322, in that we require all prime factors of consecutive numbers to have multiplicity exceeding 1.

Conclusion.

The research embodied by this paper is basic and undertaken merely out of curiosity. The question of gaps between numbers of a species, and the beginning of runs of increasing length of consecutive such numbers or numbers not of the species is one that resonates with longstanding curiosity on the part of Catalan and those who came before him. We do not expect anything earth-shaking regarding these “second-string” number theoretical species, but they do provide food for thought.

Is there a limit to the number of consecutive tantus and same of consecutive plenus numbers? The question is tied to any limit to the length of prime gaps.

Why is there an apparent resonance of many near-prime powers among arbitrary data in the sequence of first differences of multus numbers (A053707)?

Action items: the sequences C_S, C_V, D_V, L_V need to be added to OEIS if they are of general interest.

This concludes our examination.

Appendix.

Code 1: Generate large datasets of the principle omega-multiplicity species:

a1694 = With[{nn = 2^40},
Union@ Flatten@
  Table[a^2*b^3, {b, nn^(1/3)}, {a, Sqrt[nn/b^3]}]] (* Powerful *);
a246547 = Select[a1694, PrimePowerQ] (* Multus *);
a286708 = Rest@ Select[a1694, Not@*PrimePowerQ] (* Plenus *);
a126706 = Block[{k}, k = 0;
  Reap[Monitor[Do[
    If[And[#2 > 1, #1 != #2] & @@ {PrimeOmega[n], PrimeNu[n]},
    Sow[n]; Set[k, n] ], {n, 2^21}], n]][[-1, -1]]] (* Tantus *);
a120944 = Block[{k}, k = 0;
  Reap[Monitor[Do[If[And[CompositeQ[n], SquareFreeQ[n]], Sow[n]; Set[k, n] ],
  {n, 2^21}], n]][[-1, -1]]] (* Varius *);

Concerns sequences:

A000961: Prime powers: for prime p, p^ε such that ε ≥ 0.
A001221: ω(n) = number of distinct prime divisors of n.
A001222: Ω(n) = number of prime divisors of n with multiplicity.
A001223: Prime gaps: differences between consecutive primes.
A001694: Powerful numbers: A1694 = { a²b³ : a ≥ 1 ∧ b ≥ 1} = ∪({1}, A246547, A286708).
A002110: Primorials, products of the smallest n primes.
A005117: Squarefree numbers (union of primes and varius numbers).
A005250: Record gaps between primes.
A013929: Numbers that are not squarefree.
A024619: Numbers that are not prime powers.
A045882: Least m that starts a run of at least n multus numbers.
A053707: First differences of {1} ∪ A246547.
A061742: A2110(n)².
A076259: First differences of A5117.
A120944: Composite squarefree numbers (varius numbers).
A126706: Numbers neither squarefree nor prime power (tantus numbers).
A246547: Composite prime powers (multus numbers).
A286708: Numbers that are products of at least 2 multus numbers (plenus numbers).
A356322: Least m that starts a run of exactly n consecutive tantus numbers.
A358089: Tantus gaps: differences between consecutive tantus numbers.
A358173: Tantus gaps: differences between consecutive plenus numbers.
A358174: Least m that starts a run of exactly n consecutive plenus numbers.

References:

[1] M. De Vlieger, Omega multiplicity classes, Seq. Analysis, 18 May 2022.

[2] M. De Vlieger, OEIS A356322, Seq. Analysis, 28 October 2022.

Document Revision Record.

2022 1123 1200.