OEIS A341351
A sequence of Antti Karttunen.
Written by Michael Thomas De Vlieger, St. Louis, Missouri, 2021 0210.
Introduction.
We examine the sequence a(n) = A048673(A181815(n)).
Let primorial P(n) = A2110(n) = the product of the smallest n prime numbers, thus, P(4) = p1 × p2 × p3 × p4 = 2 × 3 × 5 × 7 = 210. The sequence begins:
1, 2, 6, 30, 210, 2310, 30030, 510510, 9699690, ...
We recognize the standard form of prime decomposition (D):
n = p1e1 × p2e2 × … × pwew
(integers) such that primes p1 < p2 < … < pw.
Here, w = ω(n) = A1221(n), the number of distinct primes p | n.
Define a “prime signature” M(n) as the multiset of multiplicities e seen in D(n), usually sorted greatest to least. Hence, for the number n = 504 = 2³ × 3² × 7¹ = p1³ × p2² × p4¹ (in the form where the subscript i represents π(p) = A720(p), the index of prime p), M(504) = {3, 2, 1}. We may note zeros in M(n) so as to preserve the index i of each prime, evoked according to the position in the list, hence we may list according to row n of A067255, hence, A067255(504) = {3, 2, 0, 1}. We can add any number of zeros to the list as regards prime signature, since zeros in the list represent the empty product, thus we do not list zeros in a prime signature. We note that the prime signature is tantamount to an ordered list of multiplicities of the diverse primes p | n, hence M(n) is a multiset, since we may have more than one listed multiplicity. For instance, M(10) = {1, 1}, a recipe we first encounter for n = 6; this recipe is often referred to as the squarefree semiprimes A6881, which begins, {6, 10, 14, 15, 21, 22, 26, 33, 34, 38, …}. We go on to say that M(p) = {1} and M(P(n)) presents a list of any number of 1s.
Consider s(n) = A025487(n), the sequence that lists products of primorials. As a consequence of this definition, we have numbers m that are products that are products of the smallest w = ω(s(n)) primes pie where multiplicity e > 0. We note that M(504) = {3, 2, 1} might be interpreted such that we ascribe prime power piei to the multiplicity ei found at position i, hence read the number as p1³ × p2² × p3¹ = 2³ × 3² × 5¹ = 360. We sort the multiplicities greatest to least to obtain the smallest possible m with this prime signature. Hence, n = 2025788 = 2² × 17¹ × 31³, which shares the same prime signature, would similarly boil down to 360 given the aforementioned interpretation. Therefore, the number m = 360 appears in s and is emblematic of all numbers with M(n) = {3, 2, 1}, that is, the product of a cube of a prime, a square of a different prime, and a third prime. Therefore we may also regard s(n) as a list of m that are the least numbers of a given prime signature.
Note that m in s(n) has two principal parameters, w = ω(m), the number of distinct prime divisors pi | n for 1 ≤ i ≤ w, and ℓ = A7814(m) = 2-adic valuation of m since all the prime power multiplicities e are nonincreasing as i increases.
The sequence s begins:
1, 2, 4, 6, 8, 12, 16, 24, 30, 32, 36, 48, 60, 64, 72, 96, 120, 128, 144, 180, 192, 210, ...
We note that all least terms of prime signatures, m ≤ P(k) occur in s, hence we may generate s in an algorithmic way delimited by P(k). Thus it is natural to delimit the sequence s by primorials P(k) and thus derive datasets of lengths in A098719. This sequence begins:
1, 2, 4, 9, 22, 54, 114, 246, 488, 948, 1809, 3327, 6020, 10624, 18246, 30726, 51148, 84074, 135598, 216398, 340886, 529051, 814237, 1240172, 1874464, 2817289, 4195918, 6186286, 9049492, 13121704, 18895821, 27199504, 38892092, 55318849, 78130780, 110028527, ...
We define a “multiplicity diagram” as a sort of histogram that portrays the multiplicities listed in row n of A067255 in column i for the prime power factor piei. When gcd(pi , n) = 1, we leave the column i blank.
Figure 1 is a set of labeled multiplicity diagrams that pertain to the smallest terms of s = A025487:

We note that the conjugate of M(n) or M(n)* is a list of the indices of primorials that produce n. Hence, for n = 60 = 2² × 3¹ × 5¹, with M(60) = {2, 1, 1}, the conjugate {3, 1} (for 3 primes with e ≥ 1, and 1 prime with e ≥ 2) signifies that 60 = P(3) × P(1) = 30 × 2. We may state all m in s(n) either as the product of all prime powers pie for 1 ≤ i ≤ ω(m) and e > 0, or rather, the product of primorials of a multiset of indices. The sequence A181822 transforms A025487(n) into the number m produced by interpreting M(m)* as if it were M(m). For instance, the number m = 24 = 2³ × 3¹ ⇒ 2² × 3¹ × 5¹ = 60, and conversely, 60 ⇒ 24.
It is clear that there exist some m such that M(m) is self-conjugate, meaning that M(m) = S = M(m)*. An example is m = 360 = 8 × 9 × 5 = 2³ × 3² × 5¹ = P(3) × P(2) × P(1) = 30 × 6 × 2.
Now we regard M(m)* = {k1, k2, …, kℓ} for 1 ≤ j ≤ ℓ and suppose we interpret each k instead as pk and take the product. Since the exponents ei of primes piei | m are nonincreasing as i increases, we know that ℓ = A7814(m) = 2-adic valuation of m. Hence, M(24)* = {2, 1 ,1} ⇒ p2 × p1 × p1 = 3 × 2 × 2 = 12. The greatest prime factor A6530(m) = gpf(m) is the function that converts the factors P(k) | m → pk | m'.
The sequence A181815.
We thus define the sequence A181815(n) = largest integer m such that for all d | m, A025487(n)/d = q ∈ A025487. The sequence, a permutation of the natural numbers, begins:
1, 2, 4, 3, 8, 6, 16, 12, 5, 32, 9, 24, 10, 64, 18, 48, 20, 128, 36, 15, 96, 7, 27, 40, 256, ...
In this sequence, the maxima are 2n since 2n → 2n, and the local minima are primes, since P(n) → pn.
We can create M(m) of the family F(N) of all m with N = Ω(m) prime divisors p | m (with multiplicity) via the integer partitions λk of N, i.e., the 1 ≤ k ≤ p(N) partitions λk in the entry N of A080577, where p(m) = A41(m). The canonical notation of parts ei in λk has these nonincreasing as i increases, and hence, we may indeed interpret these parts as the exponents ei in M(m) with Ω(m) = N, decoding them via m = Π_{p | n} piei. Of course, alternatively we may express m = Π_{ j=1..ℓ} Pj(kj), thereby obtaining A181815 via the product m' of the mappings P(k) → pk for all the k in M(m)*. Therefore we have bijection between m and m' wherein 2N → 2N, and P(N) → pN, and generally, what was a generally increasing transection through A025487 becomes a generally decreasing transection through A181815. This explains Antti Karttunen’s comment at A181815 seeing the plot as a “fractal spray”.
More precisely, we find the family F(N) that includes the of λk → M(m) as item tn,k in the irregular tetrahedron A036035. In the transform of A181815, we have tn,k → un,k, the latter item in the irregular tetrahedron at A333485. (This is more broadly covered here.) Therefore, for family F(N), using the transformation of A181815, we convert sn,k of A036035 to tn,k in A333485 but maintain these terms in the ordering of sn,k in A025487. As a consequence, we may refer to A098719(n) and A025488(n) as the position of primorials and powers of 2 in A025487, respectively. In A181815, we have P(n) → pn (i.e., A2110 → A40) or n in A098719, and 2n → 2n (i.e., A79 → A79) for n in A025488. Clearly, the former maxima of family F(N) become local minima of A181815, and the minima of family F(N), though they have not changed value, are now the maxima in A181815.
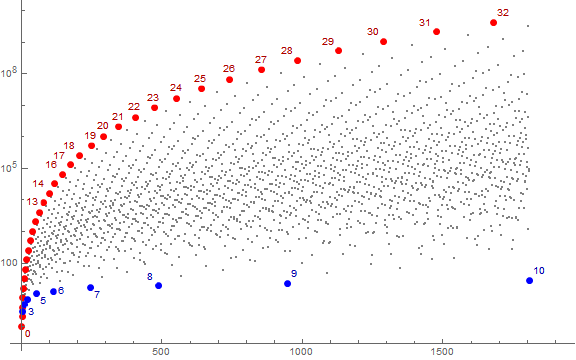
Figure 2 is a log plot of a(n) for 1 ≤ n ≤ A098719(10) = 1805, highlighting records in red, and local minima in blue. Many of the records 2N are labeled log2 a(n), while many of the local minima pN are labeled π(a(n)).
The sequence A341351.
The sequence A3961 converts piei | m → p(i+1)ei | m', while A048673 is simply the transformation Π( piei | m ) → (1 + Π( p(i+1)ei | m' ))/2. The former only has odd terms, while the latter refurnishes even terms through the inverse of the function 2x − 1.
Let a(n) = A048673(A181815(n)). We may thus simply transform Π( Pj(k) | m ) → (1 + Π( p(k+1) | m' ))/2.
The sequence begins:
1, 2, 5, 3, 14, 8, 41, 23, 4, 122, 13, 68, 11, 365, 38, 203, 32, 1094, 113, 18, 608, 6, 63, 95, 3281, 338, 53, 1823, 17, 188, 284, 9842, 1013, 158, 5468, 50, 563, 25, 851, 29525, 88, 3038, 28, 313, 473, 16403, 149, 1688, 74, 2552, 88574, 263, 9113, 7, ...
In this sequence, the maxima are (3n+ 1)/2 since, starting from A025487(n) with n in A025488, 2N → 2N → 3N → (3N+ 1)/2. Hence, A79 → A79 → A244 → A7051.
The local minima are numbers in A111333, since, starting from A025487(n) with n in A098719, P(N) → pN → p(N+1) → (p(N+1)+ 1)/2. Thus, A2110 → A40 → A6005 → A111333.
Table 1 summarizes the process of this transformation upon m in family F(5):
i n m M(m) M(m)* A181815(n) A3961(A181815(n)) A048673(A181815(n))
-------------------------------------------------------------------------------------------
1 10 32 5 -> 1.1.1.1.1 2×2×2×2×2 = 32 -> 3×3×3×3×3 = 243 -> (243+1)/2 = 122
2 12 48 4.1 -> 2.1.1.1 3×2×2×2 = 24 -> 5×3×3×3 = 135 -> (135+1)/2 = 68
3 15 72 3.2 -> 2.2.1 3×3×2 = 18 -> 5×5×3 = 75 -> (75+1)/2 = 38
4 17 120 3.1.1 -> 3.1.1 5×2×2 = 20 -> 7×3×3 = 63 -> (63+1)/2 = 32
5 20 180 2.2.1 -> 3.2 5×3 = 15 -> 7×5 = 35 -> (35+1)/2 = 18
6 29 420 2.1.1.1 -> 4.1 7×2 = 14 -> 11×3 = 33 -> (33+1)/2 = 17
7 54 2310 1.1.1.1.1 -> 5 11 = 11 -> 13 = 13 -> (13+1)/2 = 7
We anticipate that the plot of a(n) resembles the plot of many other transforms of A025487 given the bijection throughout the process, except that in the final transformation, we preserve only an apparent, relative relationship via uniform rescaling. This is because we have incremented A3961(A181815(n)) before halving.
Figure 3: Logarithmic plot of a(n) for 1 ≤ n ≤ A098719(6), labeling many points, calling out records in red and local minima in blue. (Click here for an extended plot showing 1 ≤ n ≤ A098719(8)):
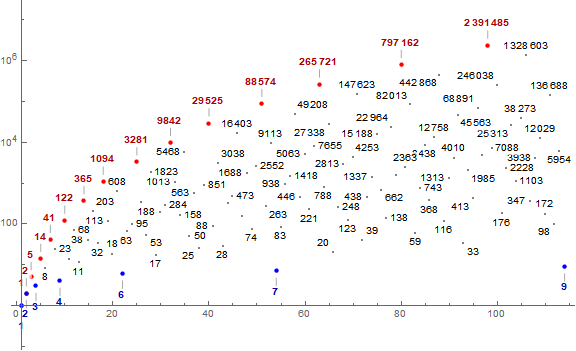
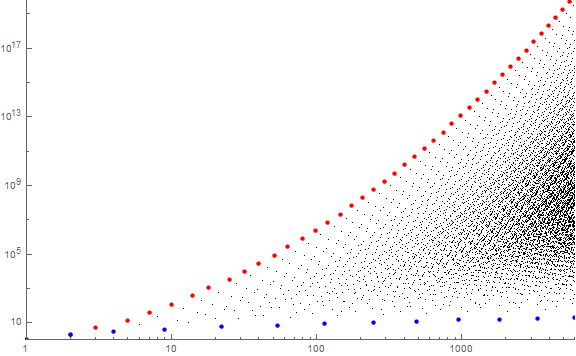
Figure 4: Log-log plot of a(n) for 1 ≤ n ≤ A098719(12), plotting records in red and local minima in blue. (Click here for an extended plot showing 1 ≤ n ≤ A098719(16)):
Let’s turn our attention on undoing the transformations so as to obtain A025487(n) from a(n).
The first step is to apply 2x − 1, hence A5408(a(n)) = A3961(A181815(n)).
The next step is to decrement the indices of the prime divisors (with multiplicity), i.e., A064989(A5408(a(n))) = A181815(n).
The third step is to take the product of the transformation pk | A181815(n) → P(k) | A025487(n). We might approach this by taking the conjugate of the multiset of indices of the prime divisors p with multiplicity, ordered greatest to least and interpreting such as multiplicity notation. Therefore, we have Π( piπ(q) ) for each qi | m listed with with multiplicity, greatest to least and 1 ≤ i ≤ Ω(m), where m is in A181815(n).
It is clear that we may use A181811(A3961(A181815(n))) = A025487(n), or A181812(A341351(n)) = A025487(n).
Appendix:
Code Toolbox: Here are a few scripts that aid in generating or analyzing this sequence:
Multiplicity notation:
A067255[n_] := If[n == 1, {0},
ReplacePart[Table[0, {PrimePi[f[[-1, 1]]]}], #] &@
Map[PrimePi@ First@ # -> Last@ # &, #]] &@ FactorInteger@ n]
(Simple) conjugate*:
conj[w_] := Table[LengthWhile[#1, # >= j &], {j, #2}] & @@ {w, Max[w]}
* This conjugate program works only in cases given nonincreasing input.
Fast generation of all terms of A025487 less than and including A2110(n)*:
A025487[n_] := {{1}}~Join~
Block[{lim = Product[Prime@ i, {i, n}],
ww = NestList[Append[#, 1] &, {1}, n - 1], dec},
dec[x_] := Apply[Times, MapIndexed[Prime[First@ #2]^#1 &, x]];
Map[Block[{w = #, k = 1},
Sort@ Prepend[If[Length@ # == 0, #, #[[1]]],
Product[Prime@ i, {i, Length@ w}] ] &@ Reap[
Do[
If[# < lim,
Sow[#]; k = 1,
If[k >= Length@ w, Break[], k++]] &@ dec@ Set[w,
If[k == 1,
MapAt[# + 1 &, w, k],
PadLeft[#, Length@ w, First@ #] &@
Drop[MapAt[# + Boole[i > 1] &, w, k], k - 1] ]],
{i, Infinity}] ][[-1]] ] &, ww]]
* Requires flattening and taking union so as to appear as a list.
a181815 = Map[Times @@ Prime@ conj@ A067255[#] &, Union@ Flatten@ A025487@ 12];
Array[If[# == 1, 1, Apply[Times, NextPrime[#1]^#2 & @@@ FactorInteger[#]]] &, 12]
Array[(1 + If[# == 1, 1, Apply[Times, NextPrime[#1]^#2 & @@@ FactorInteger[#]]])/2 &, 12]
Map[(1 + Times @@ Prime[1 + conj@ A067255[#]] /. {} -> 1)/2 &, Union@ Flatten@ A025487@ 5]
Block[{nn = 6, s, t, u, out = -100},
s = Map[(1 + Times @@ Prime[1 + conj@ A067255[#]] /. {} -> 1)/2 &,
Union@ Flatten@ A025487@ nn];
t = Union@ FoldList[Max, s];
u = Prepend[(Prime@Range[2, nn + 1] + 1)/2, 1];
t = Array[If[FreeQ[t, #], out, #] &@ s[[#]] &, Length@ s];
u = Array[If[FreeQ[u, #], out, #] &@ s[[#]] &, Length@ s];
ListPlot[{
Array[Labeled[#, #] &@ s[[#]] &, Length@ s], t, u,
Array[Callout[#, #, Above,
LabelStyle -> Directive[Bold, Darker[Red]]] &@ t[[#]] &, Length@ t],
Array[Callout[#, #, Below,
LabelStyle -> Directive[Bold, Darker[Blue]]] &@ u[[#]] &, Length@ u]},
ImageSize -> Large, ScalingFunctions -> "Log",
PlotRange -> {{1, Length@ s + 1}, {1, Max@ s}},
PlotStyle -> {
Directive[Gray, PointSize[Small]],
Directive[Red, PointSize[Medium]],
Directive[Blue, PointSize[Medium]],
Directive[Red, PointSize[Small]],
Directive[Blue, PointSize[Small]]}]
]
Concerns OEIS sequences:
A000040: The primes pn.
A000041: Number of partitions of n.
A000079:
2n.
A000244:
3n.
A002110: The primorials.
A003961: Completely multiplicative Π(
piei ) → Π( p(i+1)ei).
A005408:
The odd numbers 2n + 1.
A006005:
The odd prime numbers together with 1
A006530:
Greatest prime divisor of n, gpf(n).
A007051:
(3n+ 1)/2.
A025487: Numbers that are products of primorials, also, least m of a given prime signature.
A025488: Number of distinct prime signatures of the positive integers up to 2n.
A034386:
Product of primes q ≤ n.
A036035: Least integer of each prime signature, in graded (reflected or not) colexicographic order of exponents.
A062755: Row n = prime signature of n noting only multiplicities, where prime pk is maintained by placeholder zeros.
A080577: Row n = Integer partitions of n.
A098719: Index of the n-th primorial A2110(n) in A025487.
A108951: Primorial inflation of n: Fully multiplicative with a(p) = P(p) for prime p, where P(x) is the primorial A034386(x).
A111333:
Number of odd k ≤ pn.
A181811: Smallest integer that, upon multiplying any divisor of n, produces a member of A025487.
A181812:
Range of values of A181811, in order of first appearance: a(n) = A181811(2n −1).
A181815: Numbers where all prime divisors are consecutive primes starting at 2.
A181822: Numbers that result from interpreting M(n)* as a prime composition.
A333485:
Heinz numbers of all integer partitions sorted first by sum, then by decreasing length, and finally lexicographically.
A341351:
a(n).
A341352: Inverse permutation of a(n).
Document Revision Record.
2021 0210 1630 Draft 1.
2021 0212 1730 Final.
Click here for the index to other work.